Table of Contents
Introduction
The mathematics of cryptography can feel very daunting, but every once in a while you come across an idea that is so beautiful and elegant, yet so profoundly simple.
For me, an example for this is the Blum-Micali construction for a Cryptographically Secure Pseudo-Random Number Generator (CSPRNG) / Deterministic Random Bit Generator (DRBG) (which I think is a better name as it perfectly describes the mechanism of number generation).
The Blum-Micali algorithm is the epitome of simplicity and elegance. It creates a DRBG using purely algebraic means, using a hard-core predicate of the discrete logarithm problem.
While it is possible to generate cryptographically secure random number generators from any one-way function using the Goldreich-Levin construction, I want to emulate the elegance and simplicity of the Blum-Micali algorithm. So, in this blog, I present a toy RNG constructed in a similar fashion to the Blum-Micali DRBG but based on the hardness of a mathematical dual of the Learning with Errors (LWE) problem.
Mega Disclaimer: The algorithm described in this blog is a toy RNG. It has not been subjected to any rigorous security analysis and should be considered insecure by default.
Please do not use this for any real-world application that requires security.
Prerequisites
Pseudo-Random Number Generators
A pseudorandom number generator is an RNG algorithm that generates random-looking numbers such that no polynomial-time algorithm would be able to distinguish the output of the RNG from true randomness.
Usually, CSPRNGs take an initial seed value generated from a truly random source to generate the subsequent pseudorandom output.
Decision LWE Problem
From the above definition of PRNG, we know that the goal of an RNG is to generate an output that is indistinguishable from truly random. The Decision LWE (DLWE) problem has exactly this property.
This is the famous LWE equation
\[ b_i = a_i \cdot s + e_i \pmod q \]
Where
- $s$ (secret vector)
- A secret vector (the key) that no one knows.
- $a_i$ (public vector)
- A public vector of random numbers.
- $e_i$ (small noise)
- A small error value (+1 / 0 / -1) to smudge the result
- $q$ (prime modulus)
- A large prime number modulus
- $b_i$ (output)
- The final result, which is publicly known
The DLWE assumption states that the output $b_i$ of the LWE problem is computationally indistinguishable from a uniform random number in $\mathbb{Z}_q$.
In other words, when $s$ and $e_i$ are secret and only $a_i$ and $q$ are known publicly, the output $b_i$ is computationally indistinguishable from a random number between 0 and q-1.
Unfortunately, the LWE assumption requires use to get $a_i$ from a random uniform distribution for each sample. Since a PRNG must be entirely deterministic and reproducible from its seed, we cannot generate a truly random $a_i$ at each step, so we need to deviate from the LWE problem a bit.
Construction
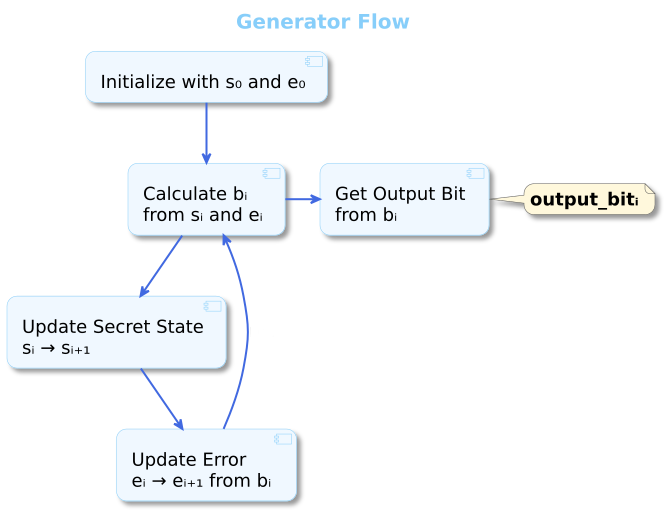
Our generator algorithm will be an iterative one. It will begin with a secret state and, in each step, it will extract one pseudorandom bit and update the state in a way that is hard to reverse. Just like the Blum-Micali algorithm.
This design has the following components:
Parameters
These are the parameters needed for the algorithm
- $q$ (prime modulus)
- A large prime number that defines our finite field \(\mathbb{Z}_q\).
- $a_0$ (seed vector)
- A vector of truly random numbers in \(\mathbb{Z}_q\). This is part of the initial seed.
- $G$ (generator matrix)
- A public, invertible square matrix used to update our secret state.
- $e_0$ (small noise)
- A small error term (+1 / 0 / -1) to smudge the answer. This is also part of the initial seed.
- $s$ (secret seed vector)
- A vector of truly random numbers that initializes our secret state. This is the the final secret input needed for entire system.
Therefore, the seed input from a true random source needed for this algorithm is $\langle a_0, s, e_0 \rangle$.
Generation Loop
To generate a stream of pseudorandom bits, we start with the initial seed is $\langle a_0, s, e_0 \rangle$. and then repeat the following four steps for each bit that we want to generate:
Step 1: Create the LWE Sample
We use the LWE equation to combine our current secret state $s$ with the vector $a_i$ and the current error $e_i$. This gives us a value $b_i$ that is indistinguishable from random.
\[ b_i = a_i \cdot s + e_i \pmod q \]
Step 2: Extract the Output Bit
Just like Blum-Micali uses a hard-core predicate, we extract a single bit from $b_i$ that is provably hard to guess. For LWE, we can use the MSB for this purpose.
\[ \text{output\_bit}_i = \lfloor \frac{2 \cdot b_i}{q} \rfloor \]
This gives us a 0 if $b_i$ is in the lower half of \(\mathbb{Z}_q\) and a 1 if it's in the upper half.
Step 3: Update the Internal State (Confusion and Diffusion)
Now, we want to update the secret state so that we can generate the next pseudorandom bit. We will incorporate Shannon's Confusion and Diffusion to thwart statistical attacks that can predict the next state from the previous state(s).
Here we use a two-step process that provides diffusion and confusion:
- Linear Mix (Diffusion): We multiply the current state by our generator matrix G. This mixes all the components of the secret vector together. \[ a'_i = G \cdot a_i \pmod q \]
- Non-linear Transform (Confusion): Here, we square each element of the mixed vector (Hadamard Product). This breaks the predictable linearity. \[ a_{i+1} = a'_i \odot a'_i \pmod q \]
Step 4: Update the Error
Finally, we need a new error term for the next iteration. To prevent the output bit from leaking information about the next error, we derive it from the low-order bits of $b_i$, which are statistically independent from the MSB we just outputted.
\[ e_{i+1} = (b_i \pmod 3) - 1 \]
This gives us a pseudorandom choice of -1, 0, or +1 for the next round.
By repeating these steps, we can generate a long sequence of pseudorandom bits from a single initial secret seed, $\langle a_0, s, e_0 \rangle$.
Example Run
To better understand the algorithm, let's walk through the first two iterations of the generator with a small set of arbitrarily chosen parameters.
Initial Parameters
\[ q = 17 \]
\[ s = \begin{pmatrix} 2 & 8 & 10 & 1 \end{pmatrix} \]
\[ a_0 = \begin{pmatrix} 9 & 5 & 4 & 1 \end{pmatrix} \]
\[ e_0 = +1 \]
\[ G = \begin{pmatrix} 2 & 3 & 3 & 8 \\ 9 & 7 & 10 & 6 \\ 0 & 12 & 8 & 8 \\ 9 & 13 & 0 & 10 \end{pmatrix} \]
Iteration 1: Generating the First Bit
Step 1: Create the LWE Sample ($b_0$)
\[ b_0 = a_0 \cdot s + e_0 \pmod q \] \[ b_0 = (9 \cdot 2 + 5 \cdot 8 + 4 \cdot 10 + 1 \cdot 1) + 1 \pmod{17} \] \[ 99 + 1 \pmod{17} \implies 100 \pmod{17} \]
Therefore \[ b_0 = 15 \]
Step 2: Extract the Output Bit
\[ output\_bit_0 = \lfloor \frac{2 \cdot 15}{17} \rfloor = \lfloor \frac{30}{17} \rfloor = 1 \] The first output bit is 1.
Step 3: Update the Internal State ($a_1$)
First, the linear mix (diffusion) with the new matrix: \[ a'_0 = G \cdot a_0 = \begin{pmatrix} 2 & 3 & 3 & 8 \\ 9 & 7 & 10 & 6 \\ 0 & 12 & 8 & 8 \\ 9 & 13 & 0 & 10 \end{pmatrix} \begin{pmatrix} 9 \\ 5 \\ 4 \\ 1 \end{pmatrix} = \begin{pmatrix} 53 \\ 162 \\ 100 \\ 156 \end{pmatrix} \pmod{17} = \begin{pmatrix} 2 \\ 9 \\ 15 \\ 3 \end{pmatrix} \] Next, the non-linear transform (confusion): \[ a_1 = a'_0 \odot a'_0 = [2^2, 9^2, 15^2, 3^2] \pmod{17} \] \[ [4, 81, 225, 9] \pmod{17} \] Our new vector is $a_1$ = [4, 13, 4, 9].
Step 4: Update the Error ($e_1$)
\[ e_1 = (b_0 \pmod 3) - 1 = (15 \pmod 3) - 1 = 0 - 1 = -1 \] The next error is $e_1$ = -1.
Iteration 2: Generating the Second Bit
Now we repeat the loop with our new state $a_1$ and error $e_1$.
Step 1: Create the LWE Sample ($b_1$)
\[ b_1 = a_1 \cdot s + e_1 \pmod q \] \[ b_1 = (4 \cdot 2 + 13 \cdot 8 + 4 \cdot 10 + 9 \cdot 1) - 1 \pmod{17} \] \[ 161 - 1 \pmod{17} \implies 160 \pmod{17} \]
Therefore \[ b_1 = 7 \]
Step 2: Extract the Output Bit
\[ output\_bit_1 = \lfloor \frac{2 \cdot 7}{17} \rfloor = \lfloor \frac{14}{17} \rfloor = 0 \] The second output bit is 0.
Step 3: Update the Internal State ($a_2$)
\[ a'_1 = G \cdot a_1 = \begin{pmatrix} 2 & 3 & 3 & 8 \\ 9 & 7 & 10 & 6 \\ 0 & 12 & 8 & 8 \\ 9 & 13 & 0 & 10 \end{pmatrix} \begin{pmatrix} 4 \\ 13 \\ 4 \\ 9 \end{pmatrix} = \begin{pmatrix} 131 \\ 221 \\ 260 \\ 295 \end{pmatrix} \pmod{17} = \begin{pmatrix} 12 \\ 0 \\ 5 \\ 6 \end{pmatrix} \] \[ a_2 = a'_1 \odot a'_1 = [12^2, 0^2, 5^2, 6^2] \pmod{17} \] \[ [144, 0, 25, 36] \pmod{17} \]
Our new secret state is $a_2$ = [8, 0, 8, 2].
Step 4: Update the Error ($e_2$)
\[ e_2 = (b_1 \pmod 3) - 1 = (7 \pmod 3) - 1 = 1 - 1 = 0 \] The next error is $e_2$ = 0.
Summary of Run
After two iterations, the generator has produced the output bitstream "10" and the internal state has evolved to $a_2$ = [8, 0, 8, 2] and $e_2$ = 0.
Interactive Demo
Here's an interactive demo written in javascript. The javascript code for this interactive demo is provided under CC0.
Interactive LWE Toy RNG
Enter the parameters below and run the generator.
Comma-separated numbers
Comma-separated numbers
Comma-separated numbers, new line for each row.
Closing Words
In this blog we have seen how to build a pseudorandom number generator from the LWE problem using a Blum-Micali style construction.
I must emphasize one last time that the spirit of this article is learning and NOT to provide an unbreakable CSPRNG. I wanted to take the elegant ideas from the Blum-Micali algorithm and apply them to the post-quantum LWE problem.
I invite you wholeheartedly to analyse and break this design.
- The output of the confusion and diffusion step may not really be a uniform random distribution as required by the LWE problem. What are the implications of using this instead?
- Can you find any statistical biases in the algorithm?
- Is it possible to recover any information about the secret state from the output bit stream?
- Is the error term $e$'s distribution in the algorithm flawed?
Thanks for reading!